1.
3 points
How many pieces of string are there in the picture?
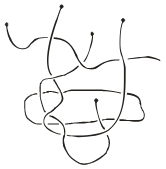
2.
In a class there are 9 boys and 13 girls. Half of the children in this class have got a cold. How many girls at least have a cold?
3.
6 kangaroos eat 6 sacks of grass in 6 minutes. How many kangaroos will eat 100 sacks of grass in 100 minutes?
4.
Numbers 2, 3, 4 and one more number are written in the cells of 2 Χ 2 table. It is known that the sum of the numbers in the first row is equal to 9, and the sum of the numbers in the second row is equal to 6. The unknown number is

5.
The triangle and the square have the same perimeter. What is the perimeter of the whole figure (a pentagon)?

6.
The florist had 24 white, 42 red and 36 yellow roses left. At most, how many identical bunches can she make, if she wants to use all the remaining flowers?
7.
A cube has all its corners cut off, as shown. How many edges does the resulting shape have?

8.
Three lines intersect in one point. Two angles are given in the figure. How many degrees is the grey angle?

9.
Demetres has 10 paper blocks with 20 sheets of paper each and Anna has 8 paper blocks with 50 sheets ofpaper each. How many paper blocks does Anna has to give to Demetres so that both have the same number of sheets
10.
How many squares can be drawn by joining the dots with line segments?

12.
Five friends have each 21, 32, 17, 11 and 16 candies. They want to give some candies to another friend. What is the minimum number of candies that they can give so that the initial group of five friends could share equally the candies between them?
13.
We write the numbers 1, 2, 3, 4, 5, 6, 7, ... consecutively around the tangent circles. We place 5 numbers on each circle. The biggest number on one circle is the same with the smallest of the tangent circle. In the figure we see some of the initial circles. What are the numbers on the 100
th circle?

14.
Tom and Jerry cut two equal rectangles. Tom got two rectangles with the perimeter of 50 cm each, and Jerry got two rectangles with the perimeter of 40 cm each. What were the perimeters of the initial rectangles?

16.
Points A, B, C and D are marked on the straight line in some order. It is known that AB= 13, BC= 11, CD= 14 and DA= 12. What is the distance between the farthest two points?
17.
Four tangent congruent circles of radius 6 cm are inscribed in a rectangle. If P is a vertex and Q and R are points of tangency, what is the area of triangle PQR?

18.
Seven cards lie in a box. Numbers from 1 to 7 are written on these cards (exactly one number on the card). The first sage takes, at random, 3 cards from the box and the second sage takes 2 cards (2 cards are left in the box). Then the first sage tells to the second one: “I know that the sum of the numbers of your cards is even”. The sum of card’s numbers of the first sage is equal to
19.
In an isosceles triangle ABC, the bisector CD of the angle C is equal to the base BC. Then the angle CDA is equal to
20.
Let ΚΛ and ΜΜ be two 2-digit numbers where Κ, Λ, Μ are pair wise different. Find ΚΛΜ if the sum ΚΛ ΜΜ+ is maximum
21.
5 points
We construct a cube with dimensions 11 x 11 x 11 from smaller cubes. What is the maximum number of small cubes that we can view from a point is space?
22.
In a company of classmates, the girls make more than 45%, but less than 50%. What is the smallest possible number of girls in that company?
23.
A boy always speaks the truth on Thursday and Fridays, always tells lies on Tuesdays, and randomly tells the truth or lies on other days of the week. On seven consecutive days he was asked what his name was, and on the first six days he gave the following answers in order: John, Bob, John, Bob, Pit, Bob. What did he answer on the seventh day?
24.
Heidi and Peter are going for a hike in the mountains. In the village they read a sign that their destination is 2 hours and 55minutes away (on foot). They leave the village at 12 o'clock. At one o'clock they sit down for their first rest and read on a different sign that the destination is only 1 hour and 15 minutes away. After a quarter of an hours' break they continue their hike at the same speed as before without any further breaks. At what time will they reach their destination?
25.
The French writer of a successful book on entertaining mathematics, Jacques Ozanam, was born after 1600 and before 1700. On year x2 he was x years old. When was he born?
26.
If κ the number of four digit natural number whose product of digits is 25 and λ the number of four digit natural numbers whose product of digits is 15, then κ/λ is equal to,
27.
Four identical dies are arranged in a row (see the fig.). The dies are not standard, i.e., the sum of points in the opposite faces of the dies not necessarily equals 7. Find the total sum of the points in all 6 touching faces of the dies.

28.
For each two digit number we substract the single digit unit from the double digit unit. If we add all the results, what is the sum?
29.
We write consecutively the numbers 1, 2, 3, 4, 5, ... with the following zink-zank method.
In which row the number 800 is located?

30.
Nina wants to complete the missing digits of the number 2 _ _ 8 with two digits so that the resulting number is divisible by 9. In how many different ways could this be accomplished?