1.
3 points questions
Among these numbers, which one is even?
2.
Where is the kangourou?

3.
How many integers are there between 19, 03 and 2,009?
4.
On the board there was an addition of numbers written but one digit was erased as shown. Which digit is the missing one?

5.
Anna has three boxes: white, red and green. One of them contains a bar of chocolate, the second contains an apple, and the third is empty. In which box we can find the chocolate, if it is known, that the chocolate is either in the white or in the red box, and the apple is neither in the white no in the green box.
6.
How many sides does this solid have (a prism with a hole)?

7.
A bridge is built across the river. The river is 120 meters wide. One quarter of the bridge is over the left river bank and one quarter of the bridge is over the right river bank. How long is the bridge?
8.
There are squares of three different sizes at the picture. The side of the smallest one is 2 metres long. What is the length of the dark marked bent line?

9.
There are cats and dogs in the room. The number of cats' paws is twice the number of dogs' noses. Then the number of cats is
10.
A kid used matches sticks to form the numbers 0 to 9, as shown in the figure. How many sticks are needed in order to form the two digit number that requires the largest number of sticks?

11.
Which of the following links requires more than one piece of rope to construct?

12.
The quadrilateral ΑΒCD has sides AB 11= m, ΒΓ7= m, Γ∆9= m and ∆Α3=m . The angles A and C are 90
o. What is the area of the quadrilateral?

13.
There are 39 green and 23 yellow birds on a tree. Every one hour 6 new green birds and 8 yellow new birds are coming to the tree. After some hours there will an equal number of green and yellow birds on the tree. How many birds in total (green and yellow) there will be at this time?
14.
Two rectangles of 8 10 and 9 12 partly cover each other. The dark grey area is 37. What is the light grey area?

15.
The number 12323314 is written on the board. John wants to erase some of the digits so that the new number that will come up will be read the same either from left to right or from right to left. What is the smallest possible number of digits that he should erase?
16.
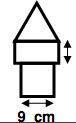
Keith had drown a Tower as shown on the figure. The Tower consists of three pieces, a square, a rectangle and an equilateral triangle. The three pieces have the same perimeter. If the side of the square is 9 cm, what is the length of the marked side of the rectangle?
17.
Kostas has a box of dimensions 30 cm length, 30 cm width and 50 cm height. He wants to fill it up with cubes that have the same size. The cubes of Kostas have side an integer number of cm. What is the minimum number of cubes that he can use?
18.
Today is Sunday. Francis begins to read a book with 290 pages. He reads 4 pages each day, except on Sundays, when he always read 25 pages, without jumping any day. How many days it took him to read the book?
19.
Andreas, Vasilis, Yiannis and Demetris have books in their bags. One of them has one book in his bag,another one has two, another has three and the last one has four books in his bag. Andreas, Vasilis and Demetris have together 6 books. Vasilis and Yiannis together have 6 books. Vasilis has in his bag less books than Andreas. Who is the one that has only one book in his bag;
20.
Helen has 18 equally sized squares. She places them side by side in order to form full rectangles. How many different rectangles can show form?
21.
5 points questions
Makis has in mind an integer number A (not zero). He said 4 statements for Α:
- It is multiple of 3.
- It is multiple of 4.
- It is multiple of 12.
- It is less than 4.
If it is known that from these statements exactly two are true and the other two are false, then A is equal to:
22.
The picture shows a solid formed with 6 triangular faces. At each vertex there is a number. For each face we consider the sum of the 3 numbers at the vertices of that face. If all the sums are the same and two of the numbers are 1 and 5 as shown, what is the sum of all the 5 numbers?

23.
A hotel has 5 floors and each floor has 35 rooms. The rooms of the first floor are numbered from 101 to 135. At the second floor they are numbered from 201 to 235, at the third 301 to 335, at the fourth from 401 to 435 and at the fifth from 501 to 535. How many times will the digit 2 be used to number the rooms?
24.
ΑΒCD is a square with side 10. The distance between Ν and Μ is 6. Each shape of the shaded part is either a square or an isosceles right triangle. Find the area of the line shaded region.

25.
In the figure the symbols

represent numbers. The sum of the digits in each row and in each column is written on the figure. What is the value of the number

?

26.
Kangaroo thinks an integer number and places it in box A. Then follows one of the possible paths indicated by arrows and perform the corresponding operations. Can Kangaroo obtain the number 2009 when arriving to the box B?

27.
A complete set of 28 dominoes contains every possible combination of two numbers of dots between 0 and 6 included, including twice the same number. How many dots are there all together on a set of dominoes?

28.
In a 4 x 2 table, two numbers are written in the first row. Each next row contains the sum and the difference of the numbers written in the previous row (see the picture for an example). In a table 7 x 2, filled in the same way, the numbers of the last row are 94 and 64. What is the sum of the numbers in the first row of the 7 x 2 table?

29.
A clock is quite strange. Firstly, it has only one hand. Every minute the hand jumps and moves five numbers further. In some occasion it was showing 12. One minute later the hand jumped to the number 5.After another one minute it jumped to 10 and so on. After how many minutes, since it was showing 12, it will show 12 again for the first time.
30.
We want to colour the squares in the grid using colours A , B , C and D in such a way that neighbouring squares do not have the same colour (squares that share a vertex are considered neighbours). Some of the squares have been coloured as shown. What are the possibilities for the shaded square?
