1.
3 points
Which is the smallest ?
2.
By what

can be replaced to have:

Χ

= 2 Χ 2 Χ 3 Χ 3 ?
3.
John(J) likes to multiply by 3, Pete(P) likes to add 2, and Nick(N) likes to subtract 1. In what order should they perform their favorite actions to convert 3 into 14?
4.
In a piece of paper there were written some number calculations, but a drop of ink made a stain and covered a number or an arithmetic symbol. Now we see the following:
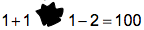
. What was at under the stain?
6.
Numbers 2, 3, 4 and one more number are written in the cells of 2 Χ 2 table. It is known that the sum of the numbers in the first row is equal to 9, and the sum of the numbers in the second row is equal to 6. The unknown number is

8.
Before the snowball fight, Paul had prepared a few snowballs. During the fight, he made another 17 snowballs and he threw 21 snowballs at the other boys. After the fight, he had 15 snowballs left. How many snowballs had Paul prepared before the fight?
9.
This is a small piece of the multiplication table.
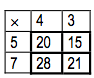
And this is an other one, in which, unfortunately, some numbers are missing.
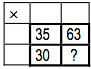
What is the number in the square with the question mark ?
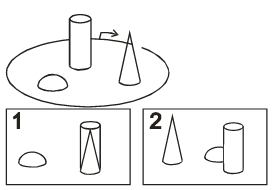
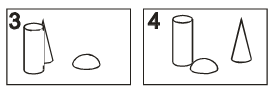
10.
In a shop selling toys a four-floor black and white “brickflower” is displayed. (picture 1). Each floor is made of bricks of the same colour. On picture 2, the flower is shown from the top. How many white bricks were used to make the flower?

11.
4 points
With what number of identical matches it is impossible to form a triangle? (The matches should not be broken!)

12.
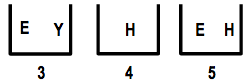
There are 5 boxes and each box contains some cards labelled A, E, H, O, Y as shown. Peter wants to remove cards from each box in such a way that at the end each box contains only one card, and different boxes contain cards with different letters. What card remains in box 2?
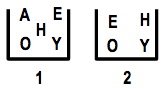
13.
The triangle and the square have the same perimeter. What is the perimeter of the whole figure (a pentagon)?

14.
A circular table is surrounded by 60 chairs. In some of the chairs there are people seating while the rest are empty. Between any two people who are seating there are two empty chairs. How many people are seating around the table?
15.
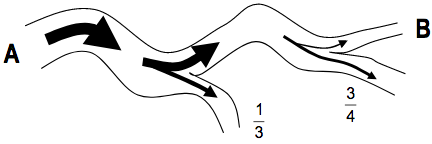
A river starts at point A. As it flows the river splits in two. One branch takes 1/3 of the water and the second takes the rest. Later the second branch splits in two, one taking 3/4 of the branch’s water, the other the rest. The map below shows the situation. What proportion of the original water flows at the point B?
16.
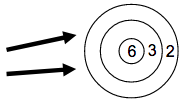
By shooting two arrows at the shown aiming board on the wall, how many different scores can we obtained? (Missing the board is possible.)
17.
Rebeka was sorting her books. The one third of her books did not fit on the shelves of her bookcase, so she put them in three drawers. In each drawer she managed to put 7 books, so again there did not fit and two books were left, which she left on the table. How many books does Rebeka have?
19.
Points A, B, C and D are marked on the straight line in some order. It is known that AB= 13, BC= 11, CD= 14 and DA= 12. What is the distance between the farthest two points?
20.
Today I can say: Two years later my son will be twice as old as he was two years ago. And three years later my daughter will be three times as old as she was three years ago. What’s right?
21.
5 points 21
The five signs @, *, #, &, ^ represent five different digits from which none is zero. They are connected through the following calculations:
@ + @ + @ = *
# + # + # = &
* + & = ^
^ = ?
What is the digit ^ ?
23.
Suppose you make a journey over the squared board shown, and you visit every square exactly once. Where must you start, if you can move only horizontally or vertically, but not diagonally?

24.
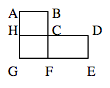
The picture shows the plan of a town. There are four circular bus routes in the town. No1 bus follows the route C-D-E-F-G-H-C, which is 17km long. No2 bus goes A-B-C-F-G-H-A, and covers 12 km. The route of No3 bus is А-B-C-D-E-F-G-H-A, and is equal to 20 km. No4 bus travels C-F-G-H-C. How long is this route?
25.
Betty walked once around the park, starting from the marked point in direction of the arrow. She made 4 photos. In which order did she make the photos?
26.
Seven cards lie in a box. Numbers from 1 to 7 are written on these cards (exactly one number on the card). The first sage takes, at random, 3 cards from the box and the second sage takes 2 cards (2 cards are left in the box). Then the first sage tells the second one: “I know that the sum of the numbers of your cards is even”. The sum of card’s numbers of the first sage is equal to
27.
Maria has drawn a picture on a piece of paper with dimensions 80cmX160cm . Afterwards she transferred the picture onto a smaller paper with dimensions 30cmX40cm. The longer side of the first picture fits exactly the longer side of the smaller. What area of the 30cmX40cm remained uncovered?


28.
How many three digit numbers are there, whose written form contains exactly two consecutive digits 3 ?
29.
We write consecutively the numbers 1, 2, 3, 4, 5, ... with the following zink-zank method.
In which row the number 800 is located?

30.
How many digits can at most be erased from the 1000-digit number 20082008...2008 (continuous repetition of 2008), such that the sum of the remaining digits is 2008?