1.
3 POINTS FOR EACH PROBLEM
If 3×2006 = 2005 + 2007 +a, then a is equal to:
2.
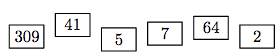
What is the greatest number we can get arranging six cards in one row, one after another, with numbers shown in the picture?
3.
There are places for 4 people at a square table, one on each side. Students put together 10 such tables, one after another, in one row so they got one rectangular table. How many places are there at the rectangular table now?
4.
There is an advertisement in a sport store:
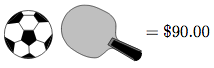

How much is a ball?
5.
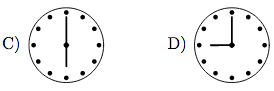
On which picture the hands of the clock form an angle with measure of 150
o?
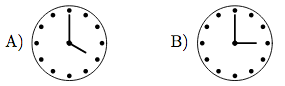
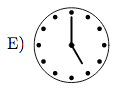
6.
On one side of Long Street there are houses numbered by consecutive odd numbers from 1 to 39, and on the other side, houses are numbered by consecutive even numbers from 2 to 34. How many houses are there on Long Street?
7.
With how many ways can you get the number 2006 while following the arrows on the figure?
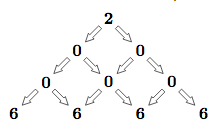
8.
A half of one one hundredth is:
10.
The square of the sum of numbers 5 and 6 decreased by their product equals:
11.
4 POINTS FOR EACH PROBLEM
Bases of four equilateral triangles are sides of a square, inwhich four circleswith radius of 5 were inscribed. The perimeter of the four-corner star in thepicture is:
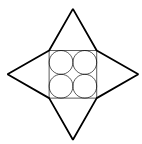
12.
What is the difference between the sum of the first 1000 consecutive, positive, even numbers and the sum of the first 1000 consecutive, positive, odd numbers?
13.
A piece of paper in the shape of a regular hexagon, as the one shown,is folded in such a way that the three marked corners touch each other at the centre of the hexagon. The obtained figure is a:
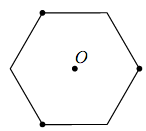
14.
To paint all sides of a cube that was built out of little cubes(Figure 1) 9 pounds of paint was used. How many pounds of paint are needed to paint the white region of the solid shown in Figure 2?

15.
A car is driving at a constant speed of 25 meters per second. How many kilometers will it travel in one hour? (1 kilometer = 1000 meters.)
16.
In rectangle ABCD,|AB|= 4 inches, and|BC|= 1 inch. Point E is the midpoint of AB, F is the midpoint of AE, G is the mid point of AD, and H is the midpoint of AG. The area of the shaded rectangle in square inches is equal to:
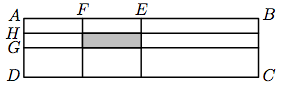
17.
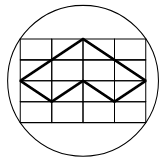
What is the result of the addition and subtraction shown on the right?

18.
The diameter of the circle in the picture is 10. What is the perimeter of the figure marked with the bold line?
19.
Six cars are parked in a parking lot in two rows. Which of the paths from S to F is the shortest?
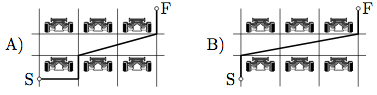
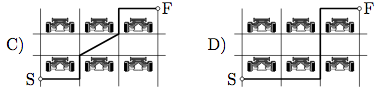
E: All are equal
20.
Anne added the biggest two-digit number divisible by 3 to the smallest two-digit number divisible by 3. Adam added the biggest two-digit number not divisible by 3 to the smallest two-digit number not divisible by 3. How much bigger is the sum that Anne calculated than the sum that Adam calculated?
21.
5 POINTS FOR EACH PROBLEM
On segment OE with a length of 2006, we place points A,B, and C so that length |OA|=|BE|= 1111 and |OC| = 70%|OE|. What is the order of points A,B, and C on the segment OE?
22.
A rope 15 inches long has been divided into the greatest possible number of pieces in such a way that each piece has a different length which is expressed by a whole number of inches. How many cuts were made?
23.
There are two islands on a river that goes through a city. There are six connecting bridges as shown in the picture. If we want to travel from point A to point B, starting the journey at bridge 1 and going through each bridge only once, then how many possible routes are there?
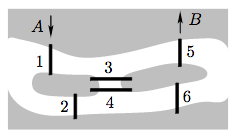
24.
Which set of three numbers represents three points on a number line where one of them is a mid point of a segment with ends represented by the other two numbers?
25.
Barbara is creating different squares with sticks of equal length. She numbers them with numbers 1, 2, 3 etc. How many more sticks will she use to create 31st square than the 30th square?
26.
There are two figures of one cube (see the picture). On each side of the cube one letter was written. On the second figure only two sides have letters on them, on the remaining sides the letters have been erased. What letter was erased from the side that was marked with the question mark?

27.
A cistern delivered gas to three different gas stations. At the first one 30% of the gas was taken out,at the second gas station 40% of the remaining gas in the cistern was taken out, and at the third stationhalf of the remaining gas was taken out. What percent of the initial amount of gas is left in the cistern?
28.
In one class18of the students received a C on the math exam,16 received a B, and 23 received an A.There were no D’s or A+’s. How many students received an F if there were less than 30 students in the class?
29.
Three friends: Adam, Tom, and Paul went to the swimming pool 15 times. Adam bought the tickets for all of them 8 times and Tom did the same 7 times. Paul gave back 30 dollars to his friends, that, as he calculated, he owed for the pool tickets. How should Adam and Tom split those 30 dollars so that each boy pays the same amount for the pool?
30.
On a blackboard, all whole numbers from 1 to 2006 were written. John underlined all numbers divisible by 2, Adam underlined all numbers divisible by 3 and Peter underlined all numbers divisible by4. How many numbers were underlined exactly twice?