1.
Problems 3 points each
A butterfly sat down on a correctly solved problem. What number did it cover up?
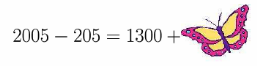
3.
Joan bought some cookies, each of which costs 3 dollars. She gave the salesperson 10 dollars, and received 1 dollar as change. How many cookies did Joan buy?
4.
After the trainer’s first whistle, the monkeys at the circus formed 4 rows. There were 4 monkeys in each row. After the second whistle, they rearranged themselves into 8 rows. How many monkeys were there in each row after the second whistle?
5.
Eva lives with her parents, her brother, one dog, two cats, two parrots, and four fish. What is the total number of legs that they have altogether?
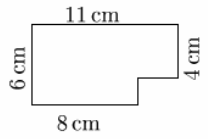
6.
John has a chocolate bar consisting of square pieces 1 cm × 1 cm in size. He has already eaten some of the corner pieces (see the picture). How many pieces does John have left?
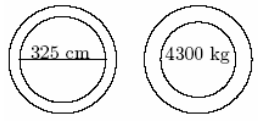
7.
Two traffic signs mark the bridge in my village (see the picture below). These signs indicate the maximum vehicle width and the maximum vehicle weight allowed on the bridge. Which one of the following trucks is allowed to cross that bridge?
8.
Each of seven boys has paid the same amount of money for a trip. The total sum of what they paid is a three digit number, which can be written as 30. What is the middle digit of this number?
9.
Problems 4 points each
What is the smallest possible number of children in a family where each child has at least one brother and at least one sister?
10.
Out of all five numbers below, I chose one. The number is even and all of its digits are different. The hundreds digit is double the ones digit. The tens digit is greater than the thousands digit. Which number did I choose?
12.
An elevator cannot carry more than 150 kg. Four friends weigh 60 kg, 80 kg, 80 kg, and 80 kg, respectively. What is the least number of trips necessary to carry the four friends to the highest floor?
13.
Ala has 24 dollars, Barb has 66 dollars, and Sophia has as many dollars more than Ala as she has less than Barb. How many dollars does Sophia have?
14.
There are eight kangaroos in the cells of the table (see the picture). What is the least number of the kangaroos that need to be moved to the empty cells so that there would be exactly two kangaroos in any row and in any column of the table?

15.
Greg needs to bring four full sacks of sand from the river to a house located at the other end of the village. Unfortunately, on his way through the village, half of the sand spills out of the sackthrough a hole. How many trips does Greg need to make from the river to the house in order to bring the required amount of sand?
16.
During a Kangaroo camp, Adam solved five problems every day, and Brad solved two problems daily. After how many days did Brad solve as many problems as Adam solved in 4 days?
17.
Problems 5 points each
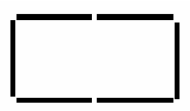
There were 9 pieces of paper. Some of them were cut into three pieces. As a result, there are 15 pieces of paper now. How many pieces of paper were cut?
18.
Using 6 matches, only one rectangle with a perimeter of 6 matches can be made (see the picture). How many different rectangles with a perimeter of 14 matches can be made using 14 matches?
19.
A picture frame was constructed using pieces of wood which all have the same width. What is the width of the frame if the inside perimeter of the frame is 8 decimeters less than its outside perimeter?
20.
In a trunk there are 5 chests, in each chest there are 3 boxes, and in each box there are 10 gold coins. The trunk, the chests, and the boxes are locked. At least how many locks need to be opened in order to take out 50 coins?
21.
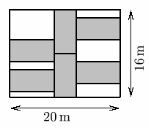
The figure shows a rectangular garden with dimensions of 16 m by 20 m. The gardener has planted six identical flowerbeds (they are gray in the diagram). What is the perimeter of each of the flowerbeds?
22.
Mike chose a three-digit number and a two-digit number. The difference of these numbers is 989. What is their sum?
23.
Five cards are laying on the table in the order: 5, 1, 4, 3, 2 as shown in the top row of the picture. They need to be placed in the order shown in the bottom row. In each move, any two cards may be switched. What is the least number of moves that need to be made?
