1.
Part A: Each correct answer is worth 3 points
A centipede has 25 pairs of shoes. It needs one shoe for each of its 100 feet. How many more shoes does the centipede need to buy?
2.
Ahmed starts counting at the number 19 and keeps counting until 89. If he takes one second to say each number how long does it take to count all the numbers?
3.
Mike cuts a pizza into quarters. Then he cuts every quarter into thirds. What part of the whole pizza is one of the pieces?
4.
Starting with 555 groups each containing 9 rocks we pile all these rocks together into one pile. We then divide this new pile into groups with 5 rocks each. How many new groups do we get?
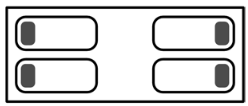
5.
On Lisa’s refrigerator 8 strong magnets (the black circles in the picture) hold some postcards.
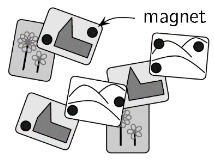
What is the greatest number of magnets Lisa could remove so that no postcard falls to the ground?
6.
Cathy draws a square of area 100 cm
2. She joins the midpoints of the sides to make a smaller square. What is the area of the smaller square?

7.
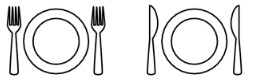
Alice’s mother wants to see a knife on the right side of each plate and a fork on the left side. What is the least number of exchanges of a knife and a fork does Alice need to make in order to please her mother?

8.
Tom and John build rectangular boxes using the same number of identical cubes.
Tom’s box looks like this:
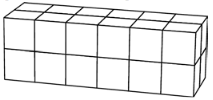
The first level of John’s box looks like this:
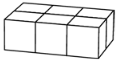
How many levels will John’s box have?
9.
On the left side of the room, Bea and Pia are sleeping with their heads on their pillows facing each other. On the right side of the room, Mary and Karen are sleeping with their heads on their pillows with their backs to each other. How many girls are sleeping with their right ear on their pillow?
10.
The piece of paper below is folded along the dotted lines to make an open box.
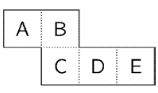
The box is put on a table with the top open. Which letter is at the bottom of the box?
11.
Part B: Each correct answer is worth 4 points
Four points A, B, C and D are given on a line, in some order, so that AB = 1, BC = 2, CD = 3, and DA = 4. Which two points are the farthest from each other?
12.
Mary, Ann, and Nata work in a kindergarten class. Each day from Monday to Friday exactly two of them come to work. Mary works 3 days per week and Ann works 4 days per week. How many days per week does Nata work?
13.
Five squirrels A, B, C, D, and E are sitting on the line. There are 6 nuts on the line as well (marked by ‘×’). At the same time, and all with the same speed, the squirrels start running to the nearest nut to them. As soon as a squirrel picks a nut it starts running to the next closest nut. Which squirrel will get two nuts?

14.
There are 30 students in a class. They sit in pairs so that each boy is sitting with a girl, and exactly half of the girls are sitting with a boy. How many boys are there in the class?
15.
The number 2581953764 is written on a strip of paper. John cuts the strip twice and gets three numbers. Then he adds these 3 numbers. What is the smallest possible sum he can get?
17.
Jennifer bought enough cat food for her four cats to last for 12 days. On her way home she brought back two stray cats. If she gives each cat the same amount of food every day, how many days will the cat food last?
18.
Tim, Tom and Jim are triplets (three brothers born on the same day), while their brother Carl is 3 years younger. Which of the following numbers could be the sum of the ages of the four brothers? (All ages are rounded to a whole year).
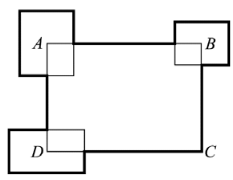
19.
The perimeter of the rectangle ABCD is 30 cm. Three other rectangles are placed so that their centres are at the points A, B, and D (see the figure). The sum of their perimeters is 20 cm. What is the total length of the thick line?
20.
Peter has 49 blue marbles and one red marble. How many marbles must Peter remove so that 90% of his marbles are blue?
21.
Part C: Each correct answer is worth 5 points
Richard is writing down all the numbers with the following properties:
- the first digit is 1;
- each of the following digits is at least as big as the one before it;
- the sum of the digits is 5.
How many numbers will he write?
22.
Luigi started a small restaurant. His friend Giacomo gave him several square tables and chairs. If he uses all the tables as single tables with 4 chairs each, he would need 6 more chairs. If he uses all the tables as double tables with 6 chairs each, he would have 4 chairs left over. How many tables did Luigi get from Giacomo?
23.
Clara wants to construct a big triangle using identical small triangular tiles. She has already put some tiles together as shown in the picture.

What is the minimum number of additional tiles required to complete a triangle?
25.
The symbols,
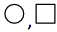
, and

represent three different digits. If you add the digits of the three-digit number

, the result is the two-digit number . If you add the digits of the two-digit number
, you get the one-digit number

. Which digit does

represent?
26.
A little Kangaroo is playing with his calculator allowing only operations on integers with an integer result. He starts with the number 12. He multiplies or divides the number by 2 or 3 (if possible) 60 times in a row. Which of the following results cannot be obtained?
27.
Two three-digit numbers have all their six digits distinct. The first digit of the second number is twice the last digit of the first number. What is the smallest possible sum of two such numbers?
28.
We want to insert the numbers 1, 2, 3, 4, 5, 6, 8, and 9 into the empty boxes below so that the sum of the numbers in each row, in each column, and in both the diagonals adds up to the same amount. What is the sum of the four numbers in the shaded boxes?
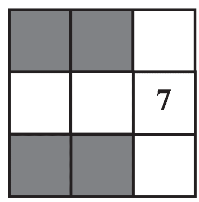
29.
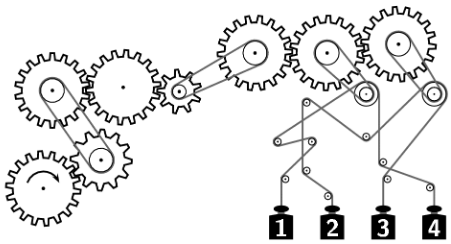
Which of the weights are going upwards when the lower left wheel is turned clockwise as indicated?