1.
Kanga can solve 6 math problems in 12 minutes. At t his rate, how many problems can she solve in 60 minutes?
2.
Minous has 16 cards: 4 spades ( ♠ ), 4 clubs ( ♣ ), 4 diamonds ( ♦ ) and 4 hearts ( ♥ ). She wants to arrange them in the square below, in such a way that every row and every column has a card of each sort. In the square below you can see how she started. What sort must be put in the square marked by the question

3.
Which of the following expressions is equal to the value of (10 × 100) × (20 × 80)?
4.
Vesna chose a whole number and multiplied it by three. Which of the following numbers could not be her answer?
6.
In one month, 5 Sundays occurred. This month could not have
7.
A rectangle has a perimeter of 24cm and one side is twice as long as another. What, in square centimetres, is the rectangle’s area?
9.
After three games of the soccer championship, Platy pus United has scored three goals and received one. They get t hree points for a win, one point for a draw and no points for a loss. How many points can they not have right now?
10.
In the addition shown on the figure the digits of t he numbers are replaced by symbols. Different symbols represent different digits, and equal symbols represent equal digits. Find the digit replaced by the square.
11.
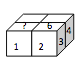
In a regular die, the faces are numbered by the num bers 1 to 6 and the sum of the numbers on any two opposite face s is 7. Nick composed a rectangular prism 2 × 2 × 1 using four identical regular dice, with the numbers on any two touching faces of the dice being equal (see the figure). The numbers on s ome faces are shown. Which number must be written on the face denoted by the ( ? )
12.
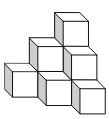
The structure shown on the picture is glued together from 10 cubes. Ryan painted the entire structure, including the bottom. How many faces of the cubes are painted?
13.
The total number of participants in a math club is between 50 and 100. The club teacher wanted to divide them in teams. He tried to group the students in 5, or 6, or 12 per team, and noticed th at there were always 3 students left. How many students are there in the math club?
14.
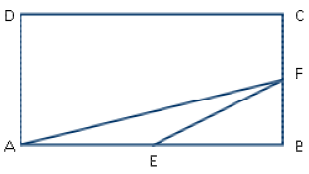
Two rectangles, ABCD and DBEF are shown in the diagram. The length of AD is 3cm; the length of AB is 4cm. What is the are a of rectangle DBEF?

15.
If you read the date 21.02 (the 21st of February) from right to left, you get 20.12, and this is also some date (the 20th of December). The date 10.09 does not possess this property (there is no 90th of January). How many dates (in the year) possess this property?
16.
In the figure, ABCD is a rectangle; E is the midpoi nt of AB; F is the midpoint of BC. What is the ratio between the area of the rectangle ABCD and the area of the triangle AEF?