2.
It takes Kanga the Kangaroo 6 seconds for every 4 jumps. How long does it take her to do 10 jumps?
3.
Zita walked from the left to the right and wrote the numbers she saw along the roads in her notepad. Which of the following groups of numbers could be the numbers written by Zita?

4.
What is the value of 2007 ÷ (2 + 0 + 0 + 7) – 2 × 0 × 0 × 7 ?
5.
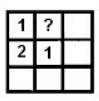
The square in the figure is a mini-sudoku : the numbers 1, 2, and 3 must be written in the cells so that each of them appears in each row and in each column. Harry started to fill in the square. In how many ways can he complete the task?
6.
Basil, who is older than Peter by one year and one day, was born on January 1, 2002. What is the date of Peter’s birthday?
December 31, 2002
December 31, 2003
7.
A robot starts walking on the table from square A2 in the direction of the arrow, as shown on the picture. It always goes forward. If it reaches a barrier, it always turns right. The robot will stop if it he cannot go forward after turning right. On which square will i t stop?
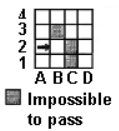
B2
A1
C3
D1
It will never stop
8.
The Carpenter’s shop has two machines A and B. A is a “printing machine” and B is a “turning machine”. What is the right sequence to ob tain Figure 1 starting from Figure 2?


BBA
ABB
BAB
BA
BABBB
9.
Part B: Each correct answer is worth 4 points.
A square is constructed on a square grid. Hanna col oured all the small squares placed on the diagonals of this square. What is the size of the side of the big square if the number of the coloured small squares is 9?
3x3
4x4
5x5
8x8
9x9
10.
Ana, Bianka, Clara, and Diana each play different s port: karate, soccer, volleyball, or judo. Ana does not like sports played with balls. The judo player Bianka often attends a soccer match to watch her friend play. Which of the follow ing statements could be true:
Ana plays volleyball
Bianka plays soccer
Clara plays volleyball
Diana plays karate
Ana plays judo
11.
Kelly has a paper ribbon 27 cm long. She divides it into four rectangles of different sizes and drew two segments such that every segment connected the centres of two adjacent rectangles (see the picture). What is the sum of the lengths of the two segments?

12 cm
13.5 cm
14 cm
14.5 cm
The answer depends on the division
12.
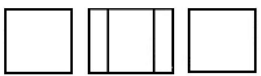
Two 9 cm × 9 cm squares overlap to form a 9 cm × 13 cm rectangle, as shown. What is the area of the region where the two squares overlap?
36 cm2
45 cm2
54 cm2
63 cm2
72 cm2
13.
There were 60 birds on three trees. At some moment 6 birds flew away from the first tree, 8 birds flew away from the second tree, and 4 birds flew away from the third tree. After that, it turned out that the number of birds on each tree was the same. How many birds were there on the second tree in the beginning?
26
24
22
21
20
14.
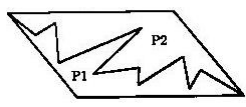
A parallelogram is divided into two parts, P1 and P 2, as shown on the picture. Which of the following statements is s urely true:
P2 has a greater perimeter than P1
P2 has a s maller perimeter than P1
P2 has a smaller area than P1
P1 and P2 have
the same perimeter
P1 and P2 have the same area
15.
What is the 2007th letter in the sequence KANGAROOKANGAROOKANG... ?
K
A
N
R
O
16.
The squares on the figure are formed by intersectin g the segment AB by the broken line AA
1A
2 ...A
12 B. The length of AB is 24 cm. What is the length of th e broken line AA
1A
2 ...A
12B?
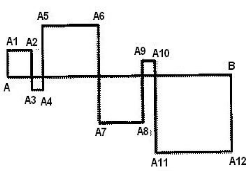
48 cm
72 cm
96 cm
56 cm
106 cm
17.
Part C: Each correct answer is worth 5 points.
Harry Potter let an owl out at 7:30 a.m. to deliver an important message to his friend Ron. The owl delivered the envelope at 9:10 a.m. An owl flies 4 km in 10 minutes. What was the distance between Harry and Ron?
14 km
20 km
40 km
56 km
64 km
18.
Bill thought of an integer number. Nick multiplied this number either by 5 or by 6. John added either 5 or 6 to Nick’s result. Last, Andrew subtracted either 5 or 6 from John’s result. The final result obtained was 73. What was Bill’s number?
10
11
12
14
15
19.
A cube with a side 1 m long has been cut into cubes of a side 1 dm each. All small cubes have been put one on top of the other, to form a ve rtical structure. What is the height of this structure?
100 m
1 km
10 km
1000 km
10 m
20.
Agnes is 10 years old. Her mother Lisa is 4 times a s old. How old will Lisa be when Agnes is twice as old as she is now?
40 years old
50 years old
60 years old
70 years old
80 years old
21.
Three diagonals are constructed on three adjacent faces of a cube, as shown on the figure. Which of the following nets is that of the given cube?

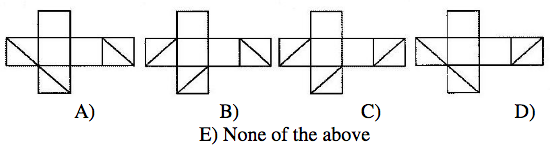
A
B
C
D
E
22.
Four paper ribbons of uniform width of 10 cm have been arranged to form figure A (see the diagram). Each of the ribbons is 25 cm longer than the previous one. The same ribbons have been rearranged to form figure B. What is the difference between the perimeters of figure A and figure B?
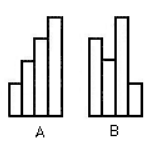
0 cm
20 cm
40 cm
50 cm
25 cm
23.
Anna wrote a 2-digit number. Ben created a 4-digit number by coping Anna's number twice. Then Anna divided Ben's number by her number. What was the result she got?
100
101
1000
1001
10
24.
Five integer numbers are written around a circle in a way that no two or three adjacent numbers have a sum divisible by 3. How many of these five numbers are divisible by 3?
0
1
2
3
Impossible to determine