1.
Part A: Each correct answer is worth 3 points
A fly has 6 legs, a spider has 8 legs. Together, 3 flies and 2 spiders have as many legs as 9 chickens and several cats. How many cats are there?
2.
Alice has 4 pieces of this shape:

. Which picture can she not make from these four pieces?
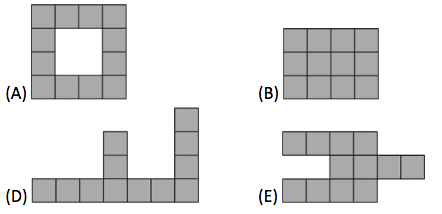
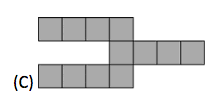
3.
Kalle knows that 1111 × 1111 = 1234321. What is the answer of 1111 × 2222?
4.
There are 10 islands and 12 bridges, as depicted in the figure. All bridges are open for traffic right now. What is the smallest number of bridges that must be closed in order to stop the traffic between A and B?
5.
Martin wants to colour the squares of the rectangle so that 1/3 of all squares are blue and half of all squares are yellow. The rest of the squares are to be coloured red.
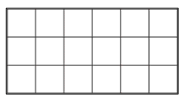
How many squares will he colour red?
6.
When the car wheels make one full rotation the car moves forward by about 1.8 meters. Approximately how many kilometres will the car move forward after 10,000 full rotations of the wheels?
7.
There are 32 students in Mrs. Vicky’s class. Part of the students took one pencil each from the box with pencils on the teacher’s desk. Then a third of the remaining students took 3 pencils each, and there were no more pencils left in the box. How many pencils were there in the box at first?
8.
Three rhinoceroses Jane, Kate and Lynn go for a walk: Jane first, Kate in the middle, and Lynn – last. Jane weighs 500 kg more than Kate. Kate weighs 1000 kg less than Lynn. Which of the following pictures may show Jane, Kate and Lynn in the order they walked?


9.
eter and Nick are both working on "Kangaroo" contest problems. For every two problems that Peter solves, Nick manages to solve three problems. In total, the boys solved 30 problems. How many problems did Nick solve more than Peter?
11.
Part B: Each correct answer is worth 4 points
A special die has a number on each of its six faces. The sums of the numbers on opposite faces are all equal. Five of the numbers are 5, 6, 9, 11 and 14. What number is on the sixth face?
12.
Tom wrote all the numbers from 1 to 20 in a row and obtained the 31‐digit number 1234567891011121314151617181920.
Then he deleted 24 of the 31 digits, so that the remaining number was as large as possible. Which number was it?
13.
Peter went hiking in the mountains for 5 days. He started on Monday and his last trip was on Friday. Each day he walked 2km more than the day before. The total distance he walked during the five days was 70km. What distance did Peter walk on Thursday?
14.
In a chocolate store, one chocolate costs $3. One day the store had a deal: “Buy two and get a third one free” and Adam decided to take 49 chocolates. How much did he pay for the chocolates?
15.
Eight kangaroos stood in a line as shown in the diagram.


At some point, two kangaroos standing side by side and facing each other exchanged places by jumping past each other. This was repeated until no further jumps were possible. How many exchanges were made?
16.
The Modern Sofa Furniture store is selling a sofa and a loveseat made from identical modular pieces as shown in the picture.
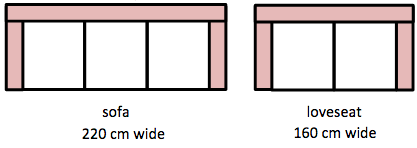
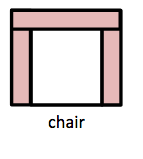
The width, including the seating and the armrests, is given below each item. How wide is an armrest?
17.
There are five padlocks and 5 keys – one for each of them (see the figure). The number code on each key has been modified into a letter code on the corresponding padlock. Equal digits have been replaced by the same letter, and different digits – by different letters. What is the number code on the fifth key?
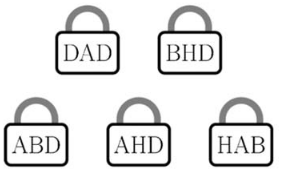
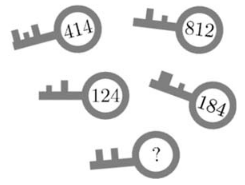
18.
Boris has an amount of money and three magic wands that he can use only once. Wand A adds $1. Wand S subtracts $1. Wand D doubles the amount. In which order must he use these wands to obtain the largest amount of money?
19.
A vase weighs 600 g when one third of it is filled with water. The same vase weighs 800 g when two thirds of it are filled with water. What is the weight of the vase when it is empty?
20.
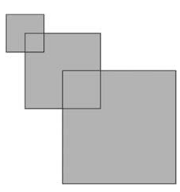
afael has three squares. The first one has side length 2 cm. The second one has side length 4 cm and a vertex is placed in the centre of the first square. The last one has side length 6 cm and a vertex is placed in the centre of the second square, as shown in the picture. What is the area of the figure?
21.
Part C: Each correct answer is worth 5 points
The natural numbers are arranged in the form of a triangle: 1 is in the first row, 2 and 3 are in the second row, 4, 5 and 6 are in the third row, and so on. What is the sum of the numbers written in the 10‐th row?
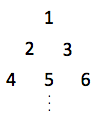
22.
There are eight balls numbered with the numbers 40, 80, 100, 101, 190, 200, 260 and 292 in a bag. Martina takes four balls out of the bag and calculates the sum of the numbers on these balls. It appears that this sum is half of the sum of the numbers on the balls that remain in the bag. What is the greatest number written on the balls taken out?
23.
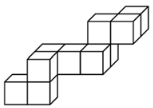
The structure on the figure is made of unit cubes glued together. Morten wants to put it into a rectangular box. What are the dimensions (length, width and height) of the smallest box he can use?
24.
Four players scored goals in a handball game. All of them scored a different number of goals. One of the players, Mike, scored the least number of goals. The other three players scored 20 goals in total. What is the largest number of goals Mike could have scored?
25.
Ala likes even numbers, Beata likes numbers divisible by 3, Celina likes numbers divisible by 5. Each of these three girls went separately to a basket containing 8 balls with numbers written on them, and took all the balls with numbers she liked. It turned out that Ala collected balls with numbers 32 and 52, Beata ‐ 24, 33 and 45, Celina ‐ 20, 25 and 35. In what order did the girls approach the basket?
27.
The numbers 1, 2, 3, 4, and 5 must be written in the five cells in the figure, respecting the following rules:
- If a number is just below another number, it must be greater.
- If a number is just to the right of another number, it must be greater. In how many ways can this be done?

28.
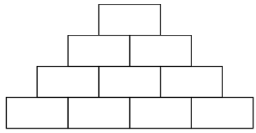
John wrote a natural number in each of the four boxes in the bottom row of the diagram. Then he wrote in each of the other boxes the sum of the two numbers in the boxes immediately underneath. What is the largest number of odd numbers that could appear in the completed diagram?
29.
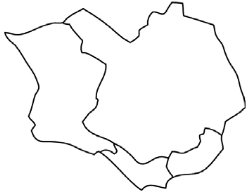
Julia has four pencils of different colours and wants to use some or all of them to paint the map of an island divided into four countries, as in the picture. Any two countries with a common border must be coloured differently on the map. How many different colourings of this map are possible? (Two colourings are considered different if at least one of the countries is coloured differently).