1.
Part A: Each correct answer is worth 3 points.
Which of the following is the greatest number?
2.
Sophie draws kangaroos: a blue one, then a green, then a red, then a black, a blue, a green, a red, a black, and so on...What colour is the 29 th kangaroo?
3.
How many integers can one find in the interval from 2.09 to 15.3?
4.
Which is the smallest positive integer divisible by 2, 3, and 4?
5.
The sum of the numbers in each ring should be 55 . What is the value of A ?

6.
Tom has 9 bills of 100 euro, 9 bills of 10 euro, and 10 coins of 1 euro. How many euro does he have in total?
7.
Betty likes calculating the sum of the digits th at she sees on her digital clock (for instance, if the clock shows 21:17, then Betty gets 11). What is the biggest sum she can get if the clock is a 24-hour clock?
8.
In the picture, AC= 10m, BD= 15m, AD= 22m. Find BC.

9.
Part B: Each correct answer is worth 4 points.
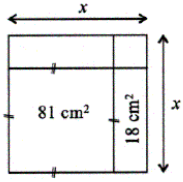
How long (in cm) is the segment denoted by x
11.
The picture shows Dave the clown dancing at the top of two balls and one cubic box. The radius of the lower ball is 6 dm, th e radius of the upper ball is three times less. The side of the cubic box is 4 dm longer than the radius of the upper ball. How high above the ground is Dave standing?

12.
The figure, shown in the picture, consists of 7 squares. Square A is the biggest one; square B – the smallest one. How many squares B can square A be divided into?

13.

14.
Benito has 20 small balls of different colours: yellow, green, blue and black. 17 of the balls are not green, 5 are black, 12 are not yellow. How many blue balls does Benito have?
15.
There are 17 trees along the road from Basil ′ s home to a pool. Basil marked some trees with a red strip as follows. On his way to his swimming le sson he has marked the first tree, and then every second tree, and on his way back, again, he has mar ked the first tree, and then every third tree. How many trees have no mark after that?
17.
Part C: Each correct answer is worth 5 points.
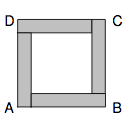
Square ABCD is comprised of one inner square (w hite) and four coloured congruent rectangles. Each coloured rectangle has a perimeter of 40 cm. What is the area of square ABCD?
18.
What date will it be exactly 2003 minutes after 20-03-2003 at 20:03
19.
A bar code is formed using 17 black and white bars (the first and last bars are black). The black bars are two types: wide and narrow. The number of white bar s is 3 more than the number of wide black bars. The number of narrow black bars is:

20.
A cylindrical glass that is 10cm high is partially filled with water. You see the glass in two positions. What is the height of the water when the glass is upright?

21.
You have six sticks of lengths 1 cm, 2 cm, 3 cm , 2001 cm, 2002 cm and 2003 cm. You have to choose three of these sticks and form a triangle. How many different choices of three sticks are there which work?
22.
Use the diagram:
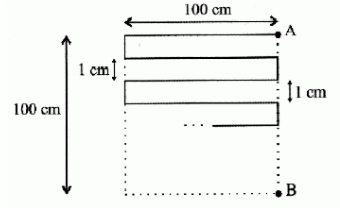
What is the length of the broken line from A to B?
23.
Here is one addition example: each shape replaces a digit, different shapes replace different digits and same shapes replace the same digit. What is the sum of the "square" and the "circle"?

24.
The figure on the drawing consists of five isosceles right triangles of equal size. Find the area of the shaded figure.
