2.
Follow the arrows and find the result.
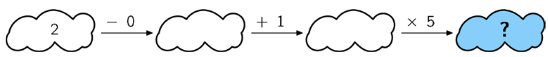
6
3.
In the figure, we see an island with a funny shape and several frogs.
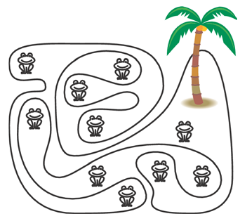
How many of these frogs are sitting on the island?
4.
Dana is saving up for skates. She puts 2 dollars in her piggy bank every Wednesday and Friday. How many dollars will she save up in five weeks?
5.
Eric had 10 equal metal strips.
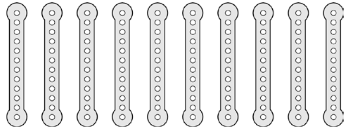
He screwed pairs of them together into five long strips as shown below.
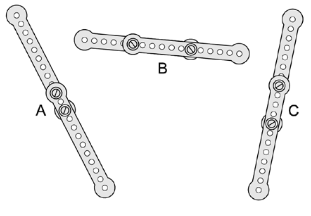
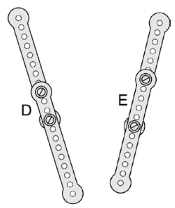
Which strip is the longest?
6.
A number has two digits. The product of the digits of this number is 15. What is the sum of the digits of this number?
9.
Part B: Each correct answer is worth 4 points
Basil wants to cut the shape in Figure 1 into identical triangles as in Figure 2.
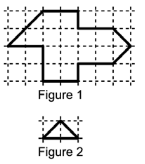
How many triangles will he get?
10.
Jack built a cube using 27 small cubes colored either grey or white (see the figure). No two of the small cubes, with the same color, have a common face. How many white cubes did Jack use?

11.
Betty marked 8 red points on a straight line. Then she put a blue point in each space between two neighbouring red points. Finally, Betty put a green point in each space between two neighbouring blue and red points. How many points did Betty mark in total?
12.
In a speed skating competition, 10 racers reached the final. Tom beat three racers more than beat him. Which place did Tom end up in?
13.
Josip has four toys - a car, a doll, a ball and a spaceship.

He wants to arrange the toys in a row on a shelf. Both the spaceship and the doll have to be next to the car. In how many ways can he arrange the toys so that the condition is fulfilled?
14.
Pete rides a bicycle in a park with bike paths asshown in the figure. He starts from the
Start line in the direction of the arrow. At the first crossroad he turns right, then at the next crossroad he turns left, then right again, then left again and so on, in that order. What is the sign which he will not pass?

15.
There are 5 ladybugs shown in the figure. Two ladybugs are friends with each other if the numbers of spots that they have differ exactly by 1. On Kangaroo Day, each of the ladybugs sent one text message to each of their friends. How many text messages were sent?

16.
A rectangle is divided into exactly 12 identical squares arranged in three rows. What is the perimeter of the rectangle, if the perimeter of one little square is 12 cm?
17.
Part C: Each correct answer is worth 5 points
Luisa wanted to fold a cube from a piece of paper. By mistake she drew and cut 7 squares on her sheet instead of 6 squares.
Which square must she remove so that the figure remains connected and Luisa can fold a cube from it?
18.
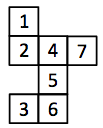
The numbers 2, 3, 5, 6 and 7 are written in the squares of the cross (see the figure) so that the sum of the numbers in the row is equal to the sum of the numbers in the column. Which of the numbers can be written in the centre square of the cross?

19.
To cook an elixir a witch needs five types of herbs exactly in the amounts weighed by the scales in the picture. The witch knows that she needs to put 5 grams of sage into the elixir. How many grams of hibiscus does she have to use? (The weight of the scales is irrelevant.)

21.
In the dotted sheet below, the distances, both horizontally and vertically, between every two neighbouring points are equal.

Ann drew all possible squares by connecting four of the points. How many different values can the area of the squares take?
22.
Tom drew a shark, a pig and a rhino and cut each of them in three pieces as shown.

Then he made different animals by combining one head, one middle part and one bottom. How many different real or fantasy animals could Tom create in total?
23.
Tom added all even numbers from 2 to 100. Alice added all odd numbers from 1 to 99. Then Joe subtracted Alice’s result from Tom’s result. What is Joe’s result?
24.
Paige has three transparent sheets with the following opaque black patterns.
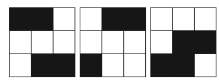
She can only rotate the sheets, she cannot flip them over. If Paige rotated the sheets and then put them one on top of the other, what would be the maximum possible number of black squares she could see if looking down on all the sheets?