2.
Calculate 2 + 2 - 2 + 2 - 2 + 2 - 2 + 2 - 2 + 2
3.
Tim got from his friends as birthday presents 10 co lour pencils, 3 matchbox cars, 4 balls, 1 book, 3 little teddy bears, and 2 chocolat es. How many things did he get?
5.
The human heart beats approximately 70 times per minute. How many beats approximately will it make in an hour?
6.
ABCD is a square. Its side is equal to 10cm. AMTD is a rectangle. Its shorter side is equal to 3 cm.
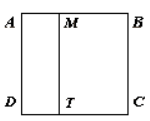
How many centimetres is the perimeter of the square ABCD larger than that of the rectangle AMTD ?
8.
Adding 17 to the smallest two-digit number and dividing the sum by the biggest one- digit number we get:
9.
Part B: Each question is worth 4 points
On one of the plates of a balance there are 6 oranges and on the other there are melons. When we put a melon exactly like the others on the orange plate, the balance is equilibrated.
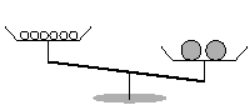
The weight of one melon is:
10.
Joseph lives on a short street the houses on that a re numbered sequentially from 1 to 24. How many times does the digit 2 occur in the numbers of those houses?
12.
During a zigzag run the kangaroos Mary, Norbert and Oscar have to jump as drawn in the picture. Suppose they jump at the same speed.
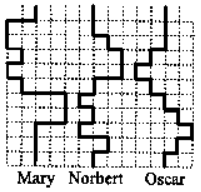
Which statement is true?
13.
Jenny, Kitty, Susan and Helen were born on March 1 st , May 17 th , July 20 th and March 20 th . Kitty and Susan were born in the same month, and Jenny’s and Susan’s birthdays fall on the same dates in different months. Who was born on May 17 th ?
14.
Samantha and Vivien have 60 matches between them. U sing some of them Samantha made a triangle whose sides had 6 matches each. Wit h all the other matches Vivien made a rectangle whose one side was also 6 matches long. How many matches long was the rectangle’s other side?
16.
28 children took part in a math league competition. The number of children who finished behind Raul was twice as large as the numb er of children who were more successful than him. In which place did Raul finish ?
18.
Julien, Manon, Nicolas and Fabienne each have a dif ferent pet: a cat, a dog, a parrot and a goldfish. Manon has a furry animal, Fabienne owns a four-legged creature, Nicolas has a bird and Manon doesn’t like cats. Whi ch statement is not true?
19.
Martina leaves her house at 6:55 a.m. and arrives a t school at 7:32 a.m. Her friend Dianne arrives at school at 7:45 a.m. even though s he lives closer to the school and it takes her 12 minutes less than Martina to get there . When does she leave her house?
20.
Robert made a tunnel using some identical cubes (fig.1). When he got bored, he rearranged the tunnel into a complete pyramid (fig. 2).
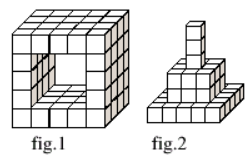
How many cubes from the original tunnel did he not use for the pyramid?
21.
The digits from 1 to 9 are written on 9 cards. Alex has the digits 7, 2 and 4; Martha has the digits 6, 5 and 1 and Fred has 8, 3 and 9. Each of them uses some of the four basic operations + (addition), - (subtraction), x (multiplication), : (division), and each of his own cards exactly once. Who cannot obtain 20 as a result?
22.
Four friends go to a restaurant and sit down at a table. John always sits at the same spot on the table. In how many ways can the friends sit around the table?
23.
Jane’s mother is making little heart-shaped cookies . For each four cookies she cuts out of the dough, there will be enough dough left t o make one extra cookie. After the first cutting she had 16 cookies. How many cookies did she make altogether?
24.
The odometer of my car indicates 187569. All the digits of this number are different. After how many more kilometres will this happen again?